Fm﹦Λr·φ1 (1)
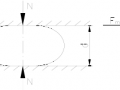
据试验资料分析显示,在刚性圆柱体沿着弹性面滚动时,由于接触区前部的压力作用会引起的力矩M:
M﹦∫b0X·P(X)dx﹦2Nb/3 (2)
式中,N 为圆柱体全长所承受的载荷;
b为接触面的1/2宽度。则:
φ1 ﹦M/R﹦2Nb/3πR (3)
将式(3)代入式(1)可得:
Fm﹦2ΛrNb/3πR (4)
又因滚动摩擦系数ƒ﹦Fm/N
则:ƒ﹦Λr·2b/3πR, (5)
其中,Λr为弹性滞后损失系数;
b为气囊的接触面的1/2宽;
R为气囊的半径。
通常情况下Λr≈3.3a,a表示在单轴拉伸压缩试验中材料的滞后损失系数。依照此式,对橡胶的单轴拉伸试验得:a﹦8%,
因此可得,Λr﹦0.264;
则:ƒ﹦0.056b/R (6)
根据力学的模型(见图2-1)。
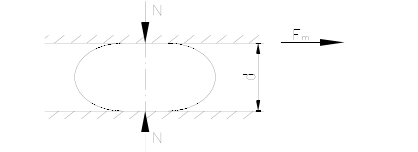
图2-1 滚动摩擦力学模型图
可得:Fm﹦2ƒN/d (7)式中:ƒ为滚动摩擦系数;
N为气囊承载;
d为气囊直径。
所以船厂在设计船台坡度的时候,通常会考虑到船舶吨位越大,由坡度产生的下滑力也会随之增大。太大的下滑力会使船舶下水速度过快,不利于施工人员操作而且增大了安全隐患,因此为了控制船舶下水时的牵引力,在设计大船的下水船台时一般选用较小的坡度。对于采用气囊下水的船舶,摩擦力起到的是阻止船舶下滑的作用。如果根据船台坡度计算的船体下滑力小于摩擦力,船舶将无法完成顺利下滑。因此,对于船舶下水,摩擦力的计算主要用于估算船舶是否能自动下滑。