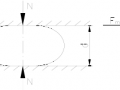
气囊压力的计算主要是解决气囊的刚度问题。
刚度是载荷与变形量的比,充以一定压力的气囊当
船舶气囊纵向下水计算方法的研究压缩高度改变时,其压缩反力会随之发生变化,其刚
度为:
K =dFdZ(1)
式中 K———气囊的刚度(kN/m);
F———气囊的承载力(kN);
Z———气囊的垂直压缩量(m)。
分析气囊压缩反力(承载力)的增量是由二部
分组成的。其一是接触面积的改变量,在平行面压
缩的情况下,接触面积的改变量基本是线性的;其二
是气囊内压的改变量,根据我们所做的试验结果,它
是非线性的。而且由于目前试验数量有限,对其变
化规律还不十分明朗。采用理论方法来求解气囊的
刚度并通过实验来验证是值得提倡的方法。
气囊充压后,由于形状改变引起的内压变化规
律应当符合理想气体方程:
(P +PA)Vn= (P0+PA)Vn0(2)
式中 P———气囊变形后的内压力(MPa);
V———气囊变形后的体积(m3);
PA———大气压力, 0. 1MPa;
P0———气囊内压的初始状态值(MPa);
V0———气囊体积的初始状态值(m3);
n———理想气体幂指数。
当气囊的变形速率较小、气体体积变化较慢时,
囊内气体可以与外界进行充分的热交换,囊内气体
的温度与外界保持一致。因此,囊内气体的变化过
程可视为等温过程,指数n=1。当气囊的变形速率
较大,囊内气体变化剧烈时,囊内气体来不及与外界
进行热交换,因此气体变化过程可视为绝热过程,n
=1.4。气囊变形速率越大,越接近绝热过程。在充
气护舷的内压计算中,日本YOKOHAMA公司的资
料建议n取1. 4。我们所做的气囊压缩性能试验曲
线也证实了这一点。只是我们的试验压缩率目前只
能做到70%左右,更高压缩率时,内压变化的规律
尚不清楚。
气囊一般都是先置于船底下再充气的,初始压
力状态也是压缩后的状态,所以按照这一算法,先要
求得初始压力时气囊压缩后的体积,再根据变形后
的体积求变形后的气囊内压。
理论计算方法的实现要作一些基本假设。其基
本假设之一是囊体周长和气囊长度在压缩变形时保
持不变;其基本假设之二是气囊囊体非受压部分呈
正规的圆形。这二个假设与实际情况是有出入的。
首先,气囊内压提高时,囊体周长和气囊长度都有不
同程度的伸张,其伸张变形的规律取决于材料特性、
帘线的布置规律和制作工艺,目前尚难以掌握;其
次,气囊非受压部分呈正规的圆形,这在囊壁较薄,
变形速率较缓的情况下容易实现,目前大型船舶下
水采用的气囊,壁厚较厚,变形后也不呈正规的圆
形。因此,理论计算的误差较大,只能通过实验得到
正确的数据。但实验由于条件受限,气囊的尺度受
到限制。所以理论计算和实验测量只能互为补充。
我们采用的压力计算方法是利用实验数据回归,并
根据实践经验加以修正得到的,由于实验数据有限,
所以建立的回归公式在今后还要不断完善,并通过
实船测量来加以验证。